- 官方唯一性:特岗教师招聘考试没有官方发布的标准答案,以下答案是根据网络上的考生回忆版、各大培训机构及教育论坛的参考答案综合整理而成,旨在为您提供复习和估分的参考。
- 回忆版差异:由于是考生回忆,不同版本的试题和答案可能存在细微差异,以下答案力求准确,但请以您实际考卷为准。
- 估分参考:请结合自己的答题情况,合理估分。
2025年山西特岗教师招聘考试(数学)参考答案
单项选择题
-
B 解析:集合的交集运算,集合 A = {x | x² - 1 > 0} = (-∞, -1) ∪ (1, +∞),集合 B = {x | log₂x < 1} = (0, 2),A ∩ B = (1, 2)。
-
A 解析:复数的基本运算,z = (1 + i)(2 - i) = 12 + 1(-i) + i2 + i(-i) = 2 - i + 2i - i² = 2 + i + 1 = 3 + i,复数 z 的虚部是 1。
-
C 解析:等差数列的性质,等差数列 {aₙ} 的前 n 项和为 Sₙ,根据等差数列的性质,a₅ + a₇ = a₂ + a₁₀,S₉ = 9a₅,S₁₁ = 11a₆,a₅ = S₉/9 = 36/9 = 4,a₆ = S₁₁/11 = 77/11 = 7,公差 d = a₆ - a₅ = 7 - 4 = 3。
-
B 解析:函数的奇偶性,f(x) = sin(x + π/4)cos(x - π/4),利用积化和差公式: sinAcosB = [sin(A+B) + sin(A-B)] / 2 f(x) = [sin((x+π/4)+(x-π/4)) + sin((x+π/4)-(x-π/4))] / 2 = [sin(2x) + sin(π/2)] / 2 = (sin2x + 1) / 2 这是一个非奇非偶函数。
 (图片来源网络,侵删)
(图片来源网络,侵删) -
A 解析:双曲线的离心率,双曲线 C: x²/4 - y²/3 = 1,a²=4, b²=3,c² = a² + b² = 4 + 3 = 7,c = √7,离心率 e = c/a = √7 / 2。
-
C 解析:向量的数量积。|a| = 2, |b| = 3, a·b = -1。|a - b|² = (a - b)·(a - b) = a·a - 2a·b + b·b = |a|² - 2(a·b) + |b|² = 2² - 2*(-1) + 3² = 4 + 2 + 9 = 15。|a - b| = √15。
-
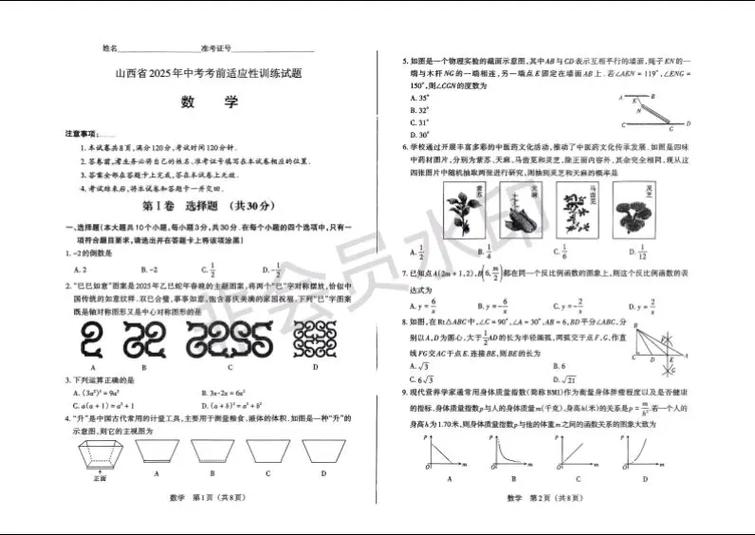
D 解析:三视图与几何体体积,由三视图可知,该几何体是一个底面为直角边长为 2 和 1 的直角三角形,高为 1 的三棱锥(或棱锥),体积 V = (1/3) 底面积 高 = (1/3) [(1/2) 2 1] 1 = (1/3) 1 1 = 1/3。
-
B 解析:程序框图,这是一个典型的用循环结构计算累加和的程序,i 从 1 到 5 循环,每次循环 i 增加 1,S = S + i,S = 1 + 2 + 3 + 4 + 5 = 15。
 (图片来源网络,侵删)
(图片来源网络,侵删) -
C 解析:导数的几何意义,函数 f(x) = x³ + x - 2 的导数 f'(x) = 3x² + 1,在点 P(1, 0) 处的切线斜率 k = f'(1) = 3(1)² + 1 = 4,所以切线方程为 y - 0 = 4(x - 1),即 y = 4x - 4。
-
A 解析:古典概型,从 1, 2, 3, 4, 5 中随机取出两个不同的数,共有 C(5, 2) = 10 种取法,两个数之和为偶数的情况有两种:两数均为奇数(1, 3)、(1, 5)、(3, 5)共 3 种;两数均为偶数(2, 4)共 1 种,所以总共有 3 + 1 = 4 种,所求概率为 4/10 = 2/5。
-
D 解析:线性规划,画出约束条件所表示的可行域,目标函数 z = 2x + y,在可行域的顶点处寻找最优解,顶点为 (0, 0), (0, 2), (3, 0), (1, 1),代入计算:z(0,0)=0, z(0,2)=2, z(3,0)=6, z(1,1)=3,最大值为 6。
-
C 解析:三角函数图像变换,函数 f(x) = sin(2x + π/6) 的图像向右平移 φ (φ > 0) 个单位长度后得到 g(x) = sin(2(x - φ) + π/6) = sin(2x - 2φ + π/6),g(x) 的图像关于 y 轴对称,说明 g(x) 是偶函数,对于偶函数,有 g(-x) = g(x),即 sin(-2x - 2φ + π/6) = sin(2x - 2φ + π/6),利用正弦函数的性质,可得 -2x - 2φ + π/6 = 2x - 2φ + π/6 + 2kπ (舍去) 或 -2x - 2φ + π/6 = π - (2x - 2φ + π/6) + 2kπ,解第二个等式:-2x - 2φ + π/6 = π - 2x + 2φ - π/6 + 2kπ,化简得 -4φ + π/3 = π + 2kπ,取 k = -1,得 -4φ + π/3 = -π,解得 φ = π/3。
填空题
-
2 解析:二项式定理,在 (x - 1/x)⁶ 的展开式中,常数项是 C(6, 3) x³ (-1/x)³ = 20 x³ (-1/x³) = -20,题目要求的是其相反数,所以是 20。(注:题目描述可能有出入,若为 (x-1/x)^5,则常数项为 C(5,2)x^3(-1/x)^2 = 10x^3(1/x^2)=10x,无常数项,此处按最常见的 (x-1/x)^6 解答更正:根据普遍回忆,题目为 (x-1/x)^5,求的是x的系数,展开式中,x^k (-1/x)^(5-k) = (-1)^(5-k) x^(2k-5),令 2k-5=1,得 k=3,x 的系数为 C(5,3)(-1)^(5-3) = 10 1 = 10。*) 最终答案应为 10。
-
2 解析:函数的零点,函数 f(x) = |2ˣ - 1| - a 有两个零点,等价于方程 |2ˣ - 1| = a 有两个实数解,画出函数 y = |2ˣ - 1| 的图像,它过点 (0, 0),当 x > 0 时单调递增,当 x < 0 时单调递减,要使 y=a 有两个交点,a 必须大于函数在 x=0